Transformarea Fourier: proprietăți, aplicații, exemple și exerciții
Transformarea Fourier este o metodă de adaptare analitică orientată spre funcțiile integrabile care aparțin familiei de transformări integrate . Se compune din redefinirea funcțiilor f (t) în termeni de Cos (t) și Sen (t).
Identitățile trigonometrice ale acestor funcții, împreună cu caracteristicile lor de derivare și antiderivare, servesc la definirea transformării Fourier prin următoarea funcție complexă:

Acest lucru este valabil atâta timp cât expresia are sens, adică atunci când integritatea necorespunzătoare este convergentă. Algebric se spune că transformarea Fourier este un homeomorfism liniar.
Orice funcție care poate fi procesată cu transformarea Fourier trebuie să aibă nulitate în afara unui parametru definit.
proprietăţi

Transformata Fourier respectă următoarele proprietăți:
existență
Pentru a verifica existența transformării Fourier într-o funcție f (t) definită în realitatea R, trebuie îndeplinite următoarele două axiome:
- f (t) este continuă în bucăți pentru toate R
- f (t) este integrat în R
Linearitatea transformării Fourier
Fie M (t) și N (t) orice două funcții cu transformări Fourier definite, cu constantele a și b, oricare.
(T)] (z) = a F (M) (z) + b F [N (t)] (z)
Care se bazează, de asemenea, pe liniaritatea integrală a aceluiași nume.
Transformarea Fourier a unui derivat
Avem o funcție f care este continuă și integrabilă în toate realitățile, unde:

Și derivatul f (f ') este continuu și definit în bucăți pe tot parcursul lui R
Transformarea Fourier a unui derivat este definită prin integrarea prin părți, prin următoarea expresie:
F [f '(t)] (z) = iz F [f (t)] (z)
În cazul derivațiilor de ordin superior, va fi aplicată într-o manieră omoloagă, unde pentru toate n 1 trebuie să:
F [f (t)] (z) = (iz) n F [f (t)] (z)
Diferențierea transformării Fourier
Avem o funcție f care este continuă și integrabilă în toate realitățile, unde:
i (d / dz) F [f (t)] (z) = F [t. f (t)] (z)
Transformarea Fourier a unei traduceri
Pentru orice element care aparține unui set S și T care aparține setului S ', trebuie:
F [ τ α] = e-iay F [ θ] F [ τ a T ] = e-iax F [ T]
Cu τ, lucrăm ca operator de traducere pe vectorul a.
Traducerea transformării Fourier
Pentru orice element care aparține unui set S și T care aparține setului S ', trebuie:
τ a F [θ] = F [e-iax . θ] τ a F [T ] = F [e-iay . T]
Pentru tot ce aparține lui R
Transformarea Fourier a unui grup de scară
Pentru toate θ care aparține unui set S. T care aparține setului S '
λ aparținând lui R - {0}, trebuie să:
F [θ (λx)] = (1 / | λ |) F [θ] ( y / λ )
F [T (λx)] = (1 / | λ |) F [T] (y / λ )
Dacă f este o funcție continuă și clar integrată, unde a> 0. Apoi:
F (f)) (z) = (1 / a) F [f (t)] (z / a)
Pentru a demonstra acest rezultat, puteți continua cu schimbarea variabilei.
Când T → + apoi s = la → + ∞
Când T → - atunci s = la → - ∞



simetrie
Pentru a studia simetria transformării Fourier, identitatea Parseval și formula Plancherel trebuie verificate.
Avem θ și δ care aparțin lui S. De aici se poate deduce că:

obținut
1 / (2π) d { F [θ ], F [δ ] } Identitatea parsevalului
1 / (2π) d / 2 || F [θ ] || Formula L 2 R d de Plancherel
Transformarea Fourier a unui produs în convoluție
Urmând obiective similare cu cele din transformarea Laplace, convoluția funcțiilor se referă la produsul dintre transformările lui Fourier.
Avem f și g ca 2 funcții limitate, definite și complet integrabile:
F (f * g) = F (f). F (g)


Apoi, atunci când schimbați variabila
t + s = x; continuă cu integritatea dublă necorespunzătoare



F (f). F (g) = F (f G)
Continuitate și cădere în infinit
Pentru orice lucru care aparține lui R, F [ θ] respectă criteriile funcției continue limitate în Rd.
De asemenea, { F [ θ] (y)} → 0 în C dacă | y | → ∞
istorie
Acest concept matematic a fost prezentat de Joseph B. Fourier în 1811 în timp ce dezvoltă un tratat privind propagarea căldurii. A fost adoptat rapid de diverse ramuri ale științei și ingineriei.
A fost stabilită ca instrument principal de lucru în studiul ecuațiilor diferențiale parțiale, chiar comparând relația de lucru dintre transformarea Laplace și ecuațiile diferențiale obișnuite.
Pentru ce este folosită transformarea Fourier?
Ea servește, în principal, la simplificarea considerabilă a ecuațiilor, transformând expresiile derivate în elemente de putere, care denotă expresii diferențiale sub formă de polinoame integrabile.
În optimizare, modelarea și modelarea rezultatelor acționează ca o expresie standardizată, fiind o resursă frecventă pentru inginerie după mai multe generații.
Seria Fourier
Acestea sunt serii definite în termeni de Cosines și Breasts; acestea servesc pentru a facilita munca cu funcții periodice generale. Când sunt aplicate, ele fac parte din tehnicile de rezolvare a ecuațiilor diferențiale parțiale și obișnuite.
Seria Fourier este chiar mai generală decât seria Taylor, deoarece dezvoltă funcții periodice discontinue care nu au reprezentare în seria Taylor.
Alte forme ale seriei Fourier
Pentru a înțelege transformarea Fourier în mod analitic, este important să examinăm celelalte forme în care se poate găsi seria Fourier, până când putem defini seria Fourier în notația complexă.
- Seria Fourier pe o funcție de perioadă de 2L
De multe ori este necesar să se adapteze structura unei serii Fourier, la funcții periodice a căror perioadă este p = 2L> 0 în intervalul [-L, L].
- Seria Fourier în funcții ciudate și uniforme
Este considerat intervalul [-π, π], care oferă avantaje atunci când profită de caracteristicile simetrice ale funcțiilor.
Dacă f este egal, seria Fourier este stabilită ca o serie de Cosines.

Dacă f este ciudat, seria Fourier este stabilită ca o serie de Sines.

- Completați notația seriei Fourier
Dacă avem o funcție f (t), care îndeplinește toate cerințele pentru dezvoltarea seriei Fourier, este posibil să o denotăm în intervalul [-t, t] folosind notația complexă:

aplicații

Calculul soluției fundamentale
Transformarea Fourier este un instrument puternic în studiul ecuațiilor diferențiale parțiale de tip liniar cu coeficienți constanți. Ei aplică pentru funcții cu domenii nelimitate în mod egal.
Ca și transformarea Laplace, transformarea Fourier transformă o funcție derivată parțială într-o ecuație diferențială obișnuită, care este mult mai simplă de a funcționa.
Problema Cauchy pentru ecuația de căldură prezintă un câmp frecvent de aplicare al transformării Fourier unde se generează funcția de căldură de bază sau nucleul Dirichlet.
În ceea ce privește calculul soluției fundamentale, sunt prezentate următoarele cazuri în care este comună găsirea transformării Fourier:
-Equation de la Laplace
-Ecuația căldurii
-Equity de Schrödinger
-Equation of wave
Teoria semnalului
Motivul general pentru aplicarea transformării Fourier în această ramificație se datorează în principal descompunerii caracteristice a unui semnal ca suprapunere infinită a semnalelor mai ușor tratabile.
Poate fi un val sonor sau un val electromagnetic, transformarea Fourier o exprimă într-o suprapunere de valuri simple. Această reprezentare este destul de frecventă în ingineria electrică.
Pe de altă parte, există exemple de aplicare a transformării Fourier în domeniul teoriei semnalului:
-Probele de identificare a sistemului. Înființată fyg
-Problem cu consistența semnalului de ieșire
-Probleme cu filtrarea semnalului
Exemple
Exemplul 1
Definiți transformarea Fourier pentru următoarea expresie:

Putem, de asemenea, să o reprezentăm în felul următor:
F (t) = Sen (t) [H (t + k) -H (t-k) ]
Impulsul rectangular este definit:
p (t) = H (t + k) -H (t-k)
Transformarea Fourier este aplicată la următoarea expresie care seamănă cu teorema modulației.
f (t) = p (t) Sen (t)
Unde: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
Și transformarea Fourier este definită de:
F (w) = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)
Exemplul 2
Definiți transformarea Fourier pentru expresia:


Deoarece f (h) este o funcție uniformă, se poate spune că


Integrarea prin părți se aplică prin selectarea variabilelor și a diferențelor lor, după cum urmează
u = sin (zh) du = z cos (zh) dh
dv = h (eh) 2 v = (eh) 2/2
Înlocuirea cu tine

După evaluarea sub teorema fundamentală a calculului

Aplicând cunoștințele anterioare privind ecuațiile diferențiale de ordinul întâi, expresia este notată ca

Pentru a obține K evaluăm

În cele din urmă, transformarea Fourier a expresiei este definită ca

Exerciții propuse
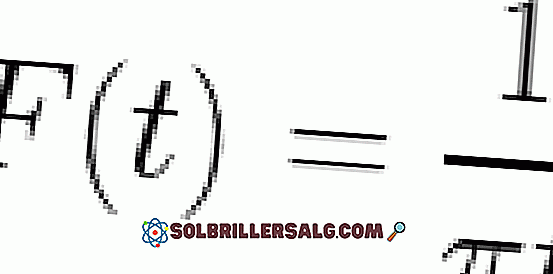

- Obțineți transformarea expresiei W / (1 + w2)